Algorithms Analysis
Algorithms Analysis
When you write a program or subprogram you should be concerned about the resource needs of the program. The two main resources to consider are time and memory. The amount of resources consumed often depends on the amount of data you have. It will also take more time for an algorithm to run. In other words what we really care about is the growth rate of resource consumption with respect to the data size.
Time Resource
Each operation that your program performs requires time. The more operations you do, the more time it will take. Thus, one way that we can measure the amount of time required by an algorithm is to measure how many operations it performs. When doing this, we make the assumption that every operation has the same time cost.
Memory Resource
This is not calculated by operation count because the number of operations doesn’t always increase memory consumption. However, we can still make a calculation on this based on variable declarations, dynamically allocated memory etc.
Growth Rates
Algorithms analysis is all about understanding growth rates. It is about understanding the growth in resource consumption as the amount of data increases. Typically, we describe the resource consumption growth rate of a piece of code in terms of a function (a “curve”).
Constant
A constant resource need is one where the resource need does not grow. That is processing 1 piece of data takes the same amount of resource as processing 1 million pieces of data. The graph of such a growth rate looks like a horizontal line.

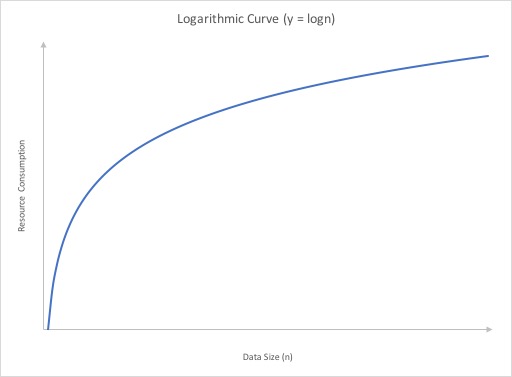
Logarithmic
A logrithmic growth rate is a growth rate where the resource needs grows by one unit each time the data is doubled. This effectively means that as the amount of data gets bigger, the curve describing the growth rate gets flatter (closer to horizontal but never reaching it). The following graph shows what a curve of this nature would look like.
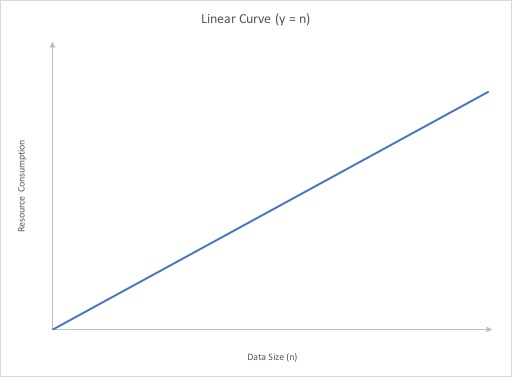
Linear
A linear growth rate is a growth rate where the resource needs and the amount of data is directly proportional to each other. That is the growth rate can be described as a straight line that is not horizontal.
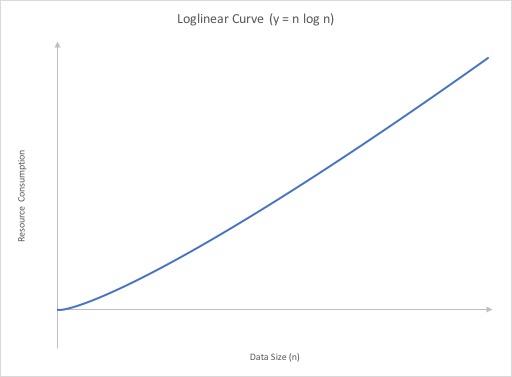
Loglinear
A loglinear growth rate is a slightly curved line. the curve is more pronounced for lower values than higher ones
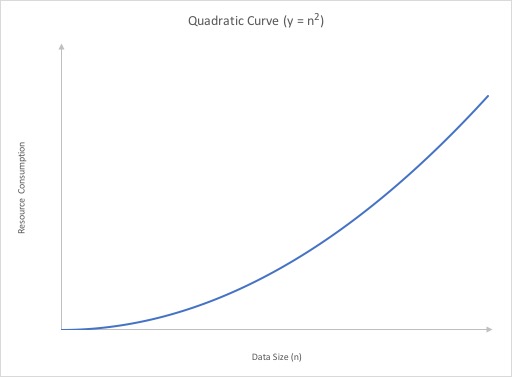
Quadratic
A quadratic growth rate is one that can be described by a parabola.
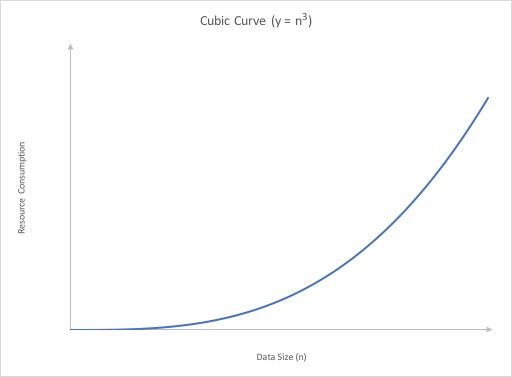
Cubic
While this may look very similar to the quadratic curve, it grows significantly
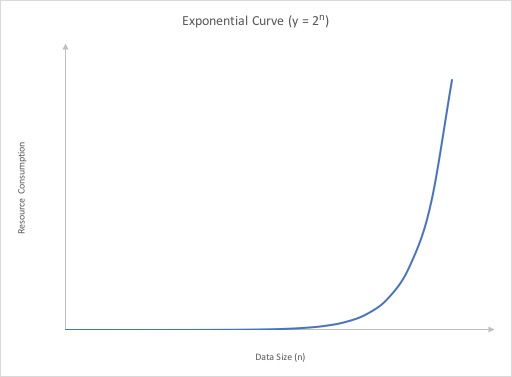
Exponential
An exponential growth rate is one where each extra unit of data requires a doubling of resource. As you can see the growth rate starts off looking like it is flat but quickly shoots up to near vertical (note that it can’t actually be vertical)
Asymptotic Notation
Asymptotic notation are formal notational methods for stating the upper and lower bounds of a function. They are the notations used when describing resource needs. These are: O() (Pronounced, Big-O, Little-O, Omega and Theta respectively). The f(n) inside each of these notations is a description of a curve like we saw in the previous section. They describe the shape of a line.
Worst case, Best Case, Average Case
The asymptotic notation system for bounds is often confused with the idea of worst case, best case and average case. They are actually very different things. Big-O does not describe a worst case, Omega does not describe a best case. Big-O describes an upper bound on each of these cases. Similarly Omega describes a lower bound on each of these cases. We should not mix up this idea.
In practice, most of the time we deal with either worst case or average case. We rarely ever consider best case. Each case can still have an upper bound(big-O) or lower bound (Omega).
5 steps
Doing mathematical analysis can be intimidating. However, what you are really doing is simply explaining a thought process. This can be done in a fairly consistent step by step manner. This section looks at the steps you should take to do this and break down how to approach an analysis.
